"Cree en ti mismo y en lo que eres. se conciente de que hay algo en tu interior que es mas grande que cualquier obstáculo --Christian D. Larson--"
miércoles, 29 de marzo de 2017
lunes, 27 de marzo de 2017
miércoles, 22 de marzo de 2017
martes, 21 de marzo de 2017
jueves, 16 de marzo de 2017
miércoles, 8 de marzo de 2017
martes, 7 de marzo de 2017
domingo, 5 de marzo de 2017
UNIDAD 2: PRINCIPIOS BÁSICOS DE LA PROBABILIDAD
INTRODUCCIÓN
El término probabilidad se asocia a los conceptos de azar y
de incertidumbre. En cualquier situación donde nos interese la aparición de
alguno de varios resultados posibles, la teoría de la probabilidad proporciona
métodos para cuantificar el grado de posibilidad de ocurrencia de cierto evento
q sea de nuestro interés. El lenguaje de probabilidad se utiliza constantemente
de una manera informal, tanto en contextos verbales como escritos. Los ejemplos
incluyen expresiones como: “es probable que el promedio de daños por sismos
disminuya significativamente, con el sistema actual de construcción anti-sísmica”,
“probablemente el próximo año egresarán por lo menos 15 estudiantes de Geociencias”,
“las probabilidades indican que una falta de asistencia a clases provoca una disminución
en calificación del alumno”, y “se espera que, con el nuevo sistema de evaluación
por sumatoria, los alumnos aprobados se incrementen en al menos 40%”.
En esta investigación se introducen algunos principios básicos
de la probabilidad, se indica como calcular las probabilidades y cómo expresar
formalmente los resultados, y como interpretar los resultados probabilísticos,
con la finalidad de poder expresar el grado de incertidumbre de un modo más
objetivo. El estudio de la probabilidad como rama de las matemáticas se remonta
a más de 300 años, y se originó para dar respuestas a preguntas vinculadas con
los juegos de azar. El objetivo de esta investigación es lograr el dominio de
los conceptos elementales de probabilidad y la habilidad para resolver cálculos
de probabilidad e interpretaciones que son necesarias para resolver los
problemas de inferencia estadística.
Origen del
estudio de la Probabilidad
- Girolamo Cardano 1501-1576
1565 - Libro de los Juegos de Azar
- Pierre de Fermat 1601-1665
- Blaise Pascal 1623-1662
1665 – Tratado sobre el
triángulo aritmético
- Christian Huygens 1629-1695
1657 – Sobre el
razonamiento relativo a los juegos de
dados
- Abraham de Moivre 1667 – 1754
1711 – Doctrina de las
Probabilidades
- Pierre Simon Laplace 1749 – 1827
1820 – Teoría Analítica
de la Probabilidad

¿Qué es la probabilidad?
- Es la rama de las matemáticas que se ocupa de medir o determinar cuantitativamente la posibilidad de que ocurra un determinado suceso. Surge con el estudio de los juegos de azar, pero se extiende a todos los fenómenos aleatorios.
- Cuando tenemos dos o más alternativas, la probabilidad nos permite de la forma más “racional o científica” posible comprender y evaluar las opciones, determinando criterios y alternativas posibles para tomar las mejores decisiones.
- Mide la frecuencia con que se obtiene un resultado bajo condiciones suficientemente estables.
- El concepto de probabilidad no es único. A través del tiempo, desde el siglo XVI en Francia debido al gran interés de los amantes de los juegos de azar y a las respuestas que querían lograr mediante la consulta a entendidos de las matemáticas, hoy se puede decir que el concepto de probabilidad admite cinco enfoques, desarrollados por expertos o escuelas que desde diferentes puntos de vista han llevado a la coexistencia de los siguientes diferentes planteamientos conceptuales, sin llegar a un acuerdo sobre cuál es el más apropiado salvo en el caso de la visión como una función matemática:
• Probabilidad frecuencial (probabilidad a posteriori)
• Probabilidad subjetiva
• Probabilidad como medida
• Probabilidad axiomática (función matemática)
¿Qué indica
la probabilidad?
- El cálculo matemático
de probabilidades se basa en situaciones teóricas en las cuales puede
configurarse un espacio muestral cuyos sucesos elementales tengan todos la
misma probabilidad.
- La probabilidad de un
resultado se representa con un número entre 0 y 1 : la probabilidad 0
indica que el resultado no ocurrirá nunca, y la probabilidad 1, que el
resultado ocurrirá siempre.
CONCEPTOS BÁSICOS
EXPERIMENTO ALEATORIO:
El término experimento se refiere a los procesos mediante los cuales se obtiene la información de
los individuos de la población estudiada, con relación a un fenómeno de interés. El resultado del
experimento, permite clasificar a los individuos observados o medidos en las categorías poblacionales
previamente definidas o bien asignarles valores numéricos.
Hay que notar que, aún cuando la idea del término “experimento” suele ser la de una situación
asociada al quehacer de científicos en un laboratorio bajo cuidadoso control, en Estadística tiene un
sentido mucho más amplio, y como se verá puede abarcar experimentos relacionados con los juegos de
azar.
ESPACIO MUESTRAL:
Los resultados asociados con un experimento aleatorio pueden provenir de observaciones (datos
categóricos), de conteos (datos numéricos discretos) o de mediciones (datos numéricos continuos). Por
ejemplo, se puede proceder a clasificar los alumnos que completan el cursado de las carreras de la
Facultad en el plazo previsto, de acuerdo al título poseído en el ingreso, o bien recabar datos sobre la
cantidad de accidentes que ocurren mensualmente en la intersección de dos calles urbanas para
justificar la instalación de un semáforo; o también, se puede experimentar midiendo el volumen de gas
que se libera en una reacción química cuando se hace variar la concentración de un ácido.
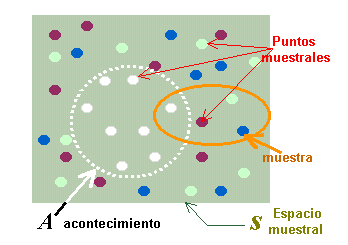
El espacio muestral, denotado con el símbolo S, es el conjunto formado por todos los posibles
resultados asociados a un experimento aleatorio. Cada uno de los posibles resultados de este espacio
muestral, recibe el nombre de punto muestral, resultado básico o elemental.
EVENTOS:
En la asignación de probabilidades a resultados experimentales, interesarán resultados
particulares del espacio muestral (puntos muestrales elementales), y también subconjuntos de
resultados pertenecientes al mismo.
Evento: En general cada uno de los posibles subconjuntos del espacio muestral de un
experimento aleatorio, recibe el nombre de evento o suceso.
Evento simple: es un evento que no se puede descomponer, por tanto corresponde a uno y solo
un punto muestral.
Evento compuesto: es un evento que se puede descomponer en al menos dos eventos simples
(está formado por al menos dos puntos muestrales). En otras palabras, el evento compuesto es
un subconjunto del S formado por al menos dos puntos muestrales.
Unión de eventos: Dados dos eventos
A
y
B de un mismo espacio muestral su
unión se representa por y es el evento que contiene los elementos que están en A o en
B, o en ambos. El evento ocurre si al menos uno
de
los
dos ocurre.
Intersección de eventos: Dados dos eventos
A
y
B de un mismo espacio
muestral su intersección se representa por A ∩ B y es el evento que contiene los elementos que están en
A
y
B
al
mismo tiempo.
TIPOS DE EVENTOS
Elemental: A cada elemento o resultado
posible del espacio muestral, se le conoce con el nombre de evento elemental.
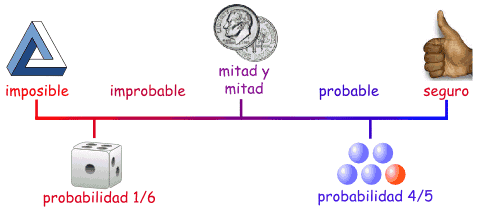
Imposible: Algunos eventos nunca pueden
ocurrir en el experimento aleatorio, y por eso se llama imposible. Se simboliza con Ø.
Seguro: Los eventos que siempre suceden
en el experimento aleatorio, son llamados eventos seguros.
Complementario: Cuando se considera un evento A,
el evento que contiene todos los eventos elementales del espacio muestral que
no estén en A se denominara Evento Complementario. Se simbolizara con Ā. Siempre que sumemos el evento A y su
complemento Ā, tendremos el espacio muestral Ω
(A + Ā = Ω).
Técnicas de
conteo
Las técnicas de conteo son aquellas que son usadas
para enumerar eventos difíciles de cuantificar y que nos proporcionan la
información de todas las maneras posibles en que ocurre un evento
determinado.
Permiten determinar el número de subconjuntos
que se pueden obtener de un conjunto. Incluye: las combinaciones, permutaciones y
los diagramas de árbol.
Principio de conteo Multiplicativo
Si se desea realizar una actividad
que consta de r pasos, en donde:
a) El primer paso de la actividad a
realizar puede ser llevado a cabo de N1 maneras o formas,
b) el segundo paso de N2 maneras
o formas
c) y el n-ésimo paso de Nn maneras
o formas,
entonces esta actividad puede ser
llevada a efecto de: N1 x N2 x ..........x Nn
maneras o formas. Cuando se trata de una sola actividad, la cual
requiere para ser llevada a efecto de una serie de pasos, entonces haremos
uso del principio multiplicativo.
Principio
de conteo Aditivo
Si se desea llevar a efecto una
actividad, la cual tiene formas alternativas para ser
realizada,
donde:
a) La primera de esas
alternativas puede ser realizada de M maneras o formas,
b) la segunda alternativa puede
realizarse de N maneras o formas .....
c) y la última de las alternativas
puede ser realizada de W maneras o formas,
entonces esa actividad puede ser
llevada a cabo de:
M + N + .........+ W maneras o
formas Si la actividad a desarrollar o a ser efectuada
tiene alternativas para ser
llevada a cabo, haremos uso del principio aditivo.
CONCLUSIÓN
Cada significado redactado
anteriormente es de suma importancia conocerlo y guardarlo en nuestra
memoria, aunque por sencillo que parezca siempre serán de utilidad, Cualquiera que sea la profesión que estemos
estudiando, una cosa es segura: tendremos la necesidad de
tomar decisiones en nuestra área laboral, tanto administrativa como de
campo, y más de la mitad de veces tendremos que hacerlo en
condiciones de incertidumbre y con un conocimiento bastante incompleto de
las consecuencias, por ello debemos tener el conocimiento mínimo de estadística y optar por la mejor decisión.
BIBLIOGRAFÍA
viernes, 3 de marzo de 2017
miércoles, 1 de marzo de 2017
domingo, 26 de febrero de 2017
UNIDAD 2: EJEMPLOS DE ESPACIOS MUESTRALES APLICADOS A GEOCIENCIAS
1) OBSERVAR EL SISTEMA CRISTALINO DE MINERALES
S= {cubico, tetragonal, hexagonal, trigonal, ortorrombico, monoclinico, triclinico}
2) TIPO DE FALLA GEOLÓGICA QUE PROVOCO UN SISMO:
S= {normal, inversa, oblicua, transcurrente}
3) PREDECIR EL CLIMA DE UN DÍA DETERMINADO EN UNA CIERTA REGIÓN SIN TENER DATOS REGISTRADOS DE DÍAS ANTERIORES:
S= {soleado, lluvioso, nublado, granizada, neblinoso}
4) TIPO DE INTEMPERISMO QUE DEGRADO UNA ROCA:
S= {químico, físico, biológico, antropico}

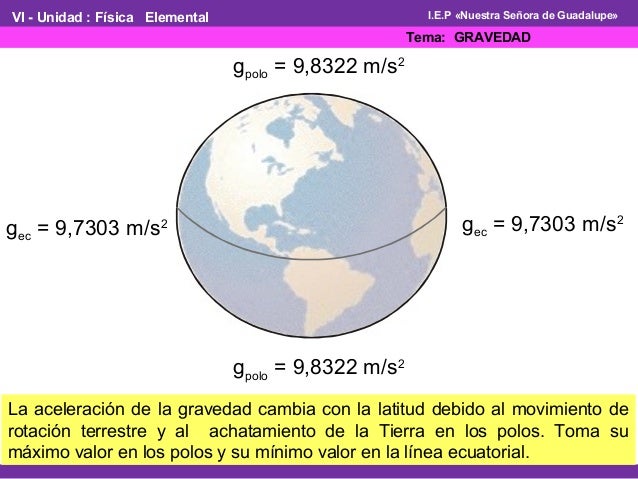
5) Determinar la gravedad terrestre en cualquier parte del mundo, sabiendo que en los polos es de 9.79 m/s^2 y en el ecuador se aproxima a los 9.83 m/s^2
S= {9.79 m/s^2,..., 9.83 m/s^2}
S= {cubico, tetragonal, hexagonal, trigonal, ortorrombico, monoclinico, triclinico}
2) TIPO DE FALLA GEOLÓGICA QUE PROVOCO UN SISMO:
S= {normal, inversa, oblicua, transcurrente}
3) PREDECIR EL CLIMA DE UN DÍA DETERMINADO EN UNA CIERTA REGIÓN SIN TENER DATOS REGISTRADOS DE DÍAS ANTERIORES:
S= {soleado, lluvioso, nublado, granizada, neblinoso}
4) TIPO DE INTEMPERISMO QUE DEGRADO UNA ROCA:
S= {químico, físico, biológico, antropico}

5) Determinar la gravedad terrestre en cualquier parte del mundo, sabiendo que en los polos es de 9.79 m/s^2 y en el ecuador se aproxima a los 9.83 m/s^2
S= {9.79 m/s^2,..., 9.83 m/s^2}

viernes, 17 de febrero de 2017
jueves, 16 de febrero de 2017
LA ESTADÍSTICA COMO UNA HERRAMIENTA
NECESARIA PARA LOS INGENIEROS GEÓLOGOS DEL FUTURO
La enseñanza de las Ciencias Básicas como
la Estadística, son
muy importantes en la formación de los ingenieros, además es un tema del cual
foros nacionales e internacionales tratan con mucha frecuencia, y en los cuales
se ha resaltado no solo el carácter formativo de las ciencias básicas, sino el
valor de éstas como una herramienta que ayuda al estudiante de ingeniería a
tener una mejor comprensión de las Ciencias de la Ingeniería en la resolución
de problemas prácticos.
Por lo regular los estudiantes de
Ingeniería en Ciencias de la Tierra, como es nuestro caso ingenieros en
Geociencias, al iniciar el camino de nuestra carrera a las Ciencias Básicas, solo
nos enfocamos a acreditar nuestras asignaturas y nos conformamos con
calificaciones mínimas sin tomarles importancia, y deseando llegar a las
materias propias de la carrera, creyendo que jamás volveremos a encontrarnos
con ecuaciones matemáticas.
El estudiante de ingeniería debe hacerse creer que es el
único responsable de su desarrollo y aprendizaje dentro y fuera del aula,
nosotros mismos debemos tener en cuenta el factor de la dimensión afectiva y
relativa al proceso de enseñanza-aprendizaje de las matemáticas para poder
entenderlas por otra parte uno de las problemáticas que presentamos es que el
curso es totalmente conceptual y eso crea en el estudiante el desinterés por la
asignatura.
El encuentro con la Estadística comienza para el estudiante
comienza en la educación primaria con la organización y clasificación de los
datos muy simples, en la educación secundaria se aprenden nuevos conceptos como
la muestra, población y los parámetros: media, moda y mediana, simplemente para
que el alumno se valla familiarizando con la verdadera estadística. En el
bachillerato ya se formaliza el estudio con un curso básico de estadística que
permite familiarizar al estudiante con algunas distribuciones más complejas,
pero no es hasta la licenciatura cuando se presentan las definiciones de las
distribuciones de manera formal desde el punto de vista matemático.
Algunas de las asignaturas que requieren de estos
conocimientos como antecedente para abordar exitosamente los cursos en la
carrera de Ingeniería Geológica son: Geometría Descriptiva Aplicada,
Geoquímica, Sedimentología, Geología Estructural, Petrología, Geología del
Subsuelo, Hidrogeología, Metalogenia, Geología Ambiental, Geología de Campo,
Tectónica, Geología Aplicada a la Ingeniería Civil, Geología del Petróleo,
Geología Aplicada a la Minería, entre otras.

Un estudio fundamental que se realiza en la Sedimentología
es el cálculo de la granulometría de un sedimento clástico, la cual es una de
las propiedades físicas más importantes de los sedimentos y de las rocas
sedimentarias, y en donde para su cálculo se realiza un análisis
granulométrico, el cual tiene como objetivo, mediante el uso de diferentes
técnicas, la separación de sedimentos de acuerdo a su tamaño, para poder
establecer de manera óptica las escalas granulométricas a las que correspondan,
y por medio de sus representaciones gráficas y parámetros estadísticos,
interpretar tentativamente los procesos y la energía de éstos que dieron origen
al depósito.
Independientemente del método de análisis granulométrico
empleado en una muestra de sedimento, tanto el método gráfico como el
estadístico son útiles para exponer los resultados, los cuales nos van a
permitir visualizar las características del sedimento. Aunque cabe mencionar
que una de las problemáticas más frecuentes al realizar dichos análisis no es
la metodología en sí, sino la interpretación gráfica y estadística de dichos
resultados.


Los datos obtenidos del análisis de tamaño de los sedimentos pueden ser utilizados de varias formas. Los gráficos son usados para representar distribuciones pictóricamente. Las curvas de frecuencia son generalmente usadas para trazar sobre papel de probabilidad cuando la interpolación exacta de las “colas” o valores dístales son necesarios para obtener los parámetros estadísticos. El trazado de las curvas permite interrelacionar muestras, diferentes y similares, para ser visualizadas en cualquier parte de su rango.
Claramente nos damos cuenta que el uso de la Estadística en la Sedimentología es muy importante, ya que nos permite realizar una adecuada interpretación gráfica y estadística de un análisis granulométrico, y no solamente es aplicable en esta área sino en muchas otras que podamos encontrar en ciencias de la tierra, donde cada un implica tanto conocimiento científico como fuente económica. para ello es necesario comprender y hacer parte de nosotros el estudio de la Estadística.
Suscribirse a:
Comentarios (Atom)